|
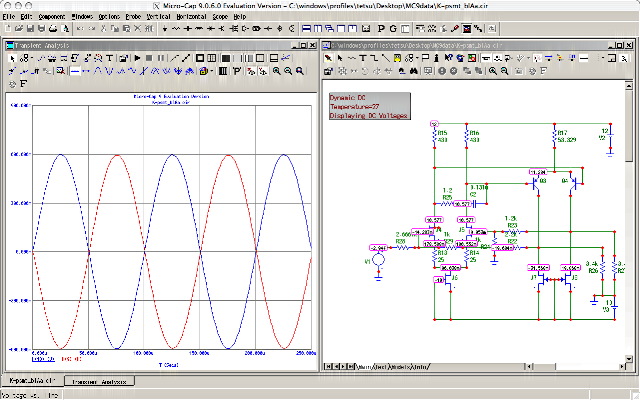
SDCのNFB定数について考えてみた
|
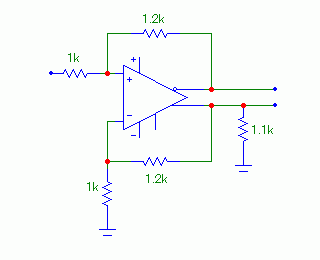 |
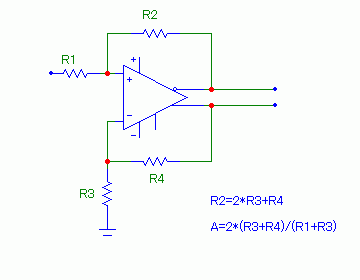
これがK式ADC前段のアナログ部、アンバランス-バランス変換部“SDC”の回路構成だ。この段の前に、おなじみの反転タイプのゲイン可変アンプが入る。 …ということで考えてみた。 このアンプの後にADCが来るので、ADCの入力の条件に合わせるため、2つの出力には約2.5VのDC電位を与えなければならない。NFBの回路定数は、その条件でアンプの+入力と-入力が等電位(2.5V×1/(1+1.2)≒1.14V)となるよう設定されている。DC的にはこれで辻褄が合っているが、1.1kがないとAC出力はアンバランスになるということだ。
|
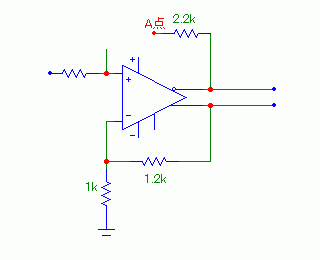 |
では、ちょっとNFBの定数を検討してみよう。話の流れをスムーズにするために、正相出力から-入力へのNFBを設定している1.2kΩと1kΩを基準にして考えることにする。 ここで、まず正相出力にはこれらを直列にした2.2kΩが負荷としてぶら下がっていて、-入力には正相出力振幅の1/(1+1.2)が加わることが分かる。 なら、とりあえず、ということで逆相出力にも負荷として2.2kΩをぶら下げてみよう。これはもちろん+入力への帰還抵抗(の一部)でもある。 さて、この2.2kΩの他端(A点)はAC的には電位が変化してもらっては困る。変化するのだったら負荷が2.2kΩにならないからだ。よって、A点をそのまま+入力に繋げるのではない。 アンプのオープンゲインがほぼ無限大であるものとして、回路全体は「2つの入力が『イマジナリーショート』すなわち同位相等振幅となるように動作する」はずだ。
|
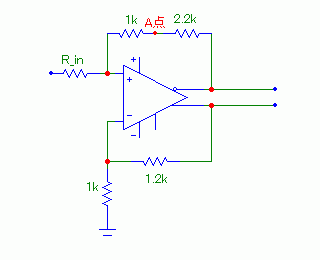 |
だったら、A点と+入力を2.2kΩの1/2.2である1kΩで結べばよいことになる。
|
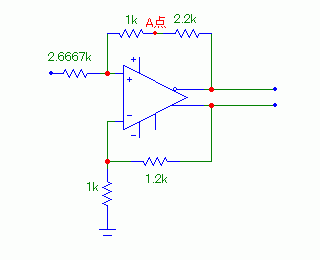 |
K式ADCのように2つの出力に2.5Vのオフセットを与える必要がある場合は、 R_in : (1k+2.2k) = 1k : 1.2k であればよいわけなので、R_in=2.667kΩとすればよい。そして、A点がAC的には0Vとなるように回路が振る舞うのであるから、入力インピーダンスは(2.667k+1k)Ωとなるはずだ。
|
つまるところ、 |
|
|
|
|
| …ということになっちゃったんですが、如何なものでしょうか。この考え方に従って定数を設定し、シミュレーションソフトで試してみたところ、どうやら一応それらしく動作するようではあります。
これが正しいのでしたら、今までの差動出力パワーアンプのNFB定数も考え直したほうがよさそうに思えますが、なにせ素人の遊びです、識者の方のチェックを乞いたいところです。
|
|